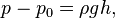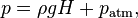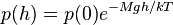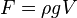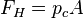Physics

Friday, September 4, 2015

Hydrostatics

Hydrostatics is the branch of fluid mechanics that studies incompressible fluids at rest. It embraces the study of the conditions under which fluids are at rest in stable equilibrium; and is contrasted with fluid dynamics, the study of fluids in motion. Hydrostatics are categorized as a part of the fluid statics, which is the study of all fluids, incompressible or not, at rest.

Hydrostatics is fundamental to hydraulics, the engineering of equipment for storing, transporting and using fluids. It is also relevant togeophysics and astrophysics (for example, in understanding plate tectonics and the anomalies of the Earth's gravitational field), tometeorology, to medicine (in the context of blood pressure), and many other fields.

Hydrostatics offers physical explanations for many phenomena of everyday life, such as why atmospheric pressure changes withaltitude, why wood and oil float on water, and why the surface of water is always flat and horizontal whatever the shape of its container.

Pressure in fluids at rest[edit]

Due to the fundamental nature of fluids, a fluid cannot remain at rest under the presence of a shear stress. However, fluids can exert pressure normal to any contacting surface. If a point in the fluid is thought of as an infinitesimally small cube, then it follows from the principles of equilibrium that the pressure on every side of this unit of fluid must be equal. If this were not the case, the fluid would move in the direction of the resulting force. Thus, the pressure on a fluid at rest is isotropic; i.e., it acts with equal magnitude in all directions. This characteristic allows fluids to transmit force through the length of pipes or tubes; i.e., a force applied to a fluid in a pipe is transmitted, via the fluid, to the other end of the pipe. This principle was first formulated, in a slightly extended form, by Blaise Pascal, and is now called Pascal's law.

Hydrostatic pressure[edit]

See also: Vertical pressure variation

In a fluid at rest, all frictional stresses vanish and the state of stress of the system is called hydrostatic. When this condition of (V=0) is applied to the Navier-Stokes equation, the gradient of pressure becomes a function of body forces only. For a Barotropic fluid in a conservative force field like a gravitational force field, pressure exerted by a fluid at equilibrium becomes a function of force exerted by gravity.

The hydrostatic pressure can be determined from a control volume analysis of an infinitesimally small cube of fluid. Since pressure is defined as the force exerted on a test area (p= F/A, with p: pressure, F: force normal to area A, A: area), and the only force acting on any such small cube of fluid is the weight of the fluid column above it, hydrostatic pressure can be calculated according to the following formula:

p(z)-p(z_0)=\frac{1}{A}\int_{z_0}^z dz' \iint\limits_A dx' dy'\, \rho (z') g(z') = \int_{z_0}^z dz'\, \rho (z') g(z')

where:

p is the hydrostatic pressure (Pa),
ρ is the fluid density (kg/m³),
g is gravitational acceleration (m/s²),
A is the test area (m²),
z is the height (parallel to the direction of gravity) of the test area (m),
z₀ is the height of the zero reference point of the pressure (m).

For water and other liquids, this integral can be simplified significantly for many practical applications, based on the following two assumptions: Since many liquids can be considered incompressible, a reasonably good estimation can be made from assuming a constant density throughout the liquid. (The same assumption cannot be made within a gaseous environment.) Also, since the height h of the fluid column between z and z₀ is often reasonably small compared to the radius of the Earth, one can neglect the variation ofg. Under these circumstances, the integral boils down to the simple formula:

\ p - p_0 = \rho g h,

where h is the height z − z₀ of the liquid column between the test volume and the zero reference point of the pressure. Note that this reference point should lie at or below the surface of the liquid. Otherwise, one has to split the integral into two (or more) terms with the constant ρ_liquid and ρ(z')_above. For example, the absolute pressure compared to vacuum is:

\ p = \rho g H + p_\mathrm{atm},

where H is the total height of the liquid column above the test area to the surface, and p_atm is the atmospheric pressure, i.e., the pressure calculated from the remaining integral over the air column from the liquid surface to infinity. This can easily be visualized using a Pressure prism.

Hydrostatic pressure has been used in the preservation of foods in a process called pascalization.^[2]

Medicine[edit]

In medicine, hydrostatic pressure in blood vessels is the pressure of the blood against the wall. It is the opposing force to oncotic pressure.

Atmospheric pressure[edit]

Statistical mechanics shows that, for a gas of constant temperature, T, its pressure, p will vary with height, h, as:

\ p (h)=p (0) e^{-Mgh/kT}

where:

g is the acceleration due to gravity
T is the absolute temperature
k is Boltzmann constant
M is the mass of a single molecule of gas
p is the pressure
h is the height

This is known as the barometric formula, and may be derived from assuming the pressure is hydrostatic.

If there are multiple types of molecules in the gas, the partial pressure of each type will be given by this equation. Under most conditions, the distribution of each species of gas is independent of the other species.

Buoyancy[edit]

Any body of arbitrary shape which is immersed, partly or fully, in a fluid will experience the action of a net force in the opposite direction of the local pressure gradient. If this pressure gradient arises from gravity, the net force is in the vertical direction opposite that of the gravitational force. This vertical force is termed buoyancy or buoyant force and is equal in magnitude, but opposite in direction, to the weight of the displaced fluid. Mathematically,

F = \rho g V

where ρ is the density of the fluid, g is the acceleration due to gravity, and V is the volume of fluid directly above the curved surface.^[3] In the case of a ship, for instance, its weight is balanced by pressure forces from the surrounding water, allowing it to float. If more cargo is loaded onto the ship, it would sink more into the water – displacing more water and thus receive a higher buoyant force to balance the increased weight.

Discovery of the principle of buoyancy is attributed to Archimedes.

Hydrostatic force on submerged surfaces[edit]

The horizontal and vertical components of the hydrostatic force acting on a submerged surface are given by the following:^[3]

F_H = p_cA

F_V = \rho g V

where:

p_c is the pressure at the center of the vertical projection of the submerged surface
A is the area of the same vertical projection of the surface
ρ is the density of the fluid
g is the acceleration due to gravity
V is the volume of fluid directly above the curved surface

Liquids (fluids with free surfaces)[edit]

What is Physics?

Physics is the natural science that involves the study of matter^[4] and its motion through space and time, along with related concepts such as energy and force.^[5] More broadly, it is the general^{[disputed – discuss]} analysis of nature, conducted in order to understand how the universe behaves.^[a]^[6]^[7]^[8]

Physics is one of the oldest academic disciplines, perhaps the oldest through its inclusion of astronomy.^[9] Over the last two millennia, physics was a part of natural philosophy along with chemistry, certain branches of mathematics, and biology, but during the scientific revolution in the 17th century, the natural sciences emerged as unique research programs in their own right.^[b] Physics intersects with many interdisciplinary areas of research, such as biophysics and quantum chemistry, and the boundaries of physics are not rigidly defined. New ideas in physics often explain the fundamental mechanisms of other sciences^[6] while opening new avenues of research in areas such as mathematics and philosophy.

Physics also makes significant contributions through advances in new technologies that arise from theoretical breakthroughs. For example, advances in the understanding of electromagnetism or nuclear physics led directly to the development of new products that have dramatically transformed modern-day society, such as television, computers, domestic appliances, and nuclear weapons;^[6] advances in thermodynamics led to the development of industrialization, and advances in mechanics inspired the development of calculus.

Steam Engine

A steam engine is a heat engine that performs mechanical work using steam as its working fluid.

Using boiling water to produce mechanical motion goes back over 2000 years, but early devices were not practical. The Spanish inventorJerónimo de Ayanz y Beaumont patented in 1606 the first steam engine. In 1698 Thomas Savery patented a steam pump that used steam in direct contact with the water being pumped. Savery's steam pump used condensing steam to create a vacuum and draw water into a chamber, and then applied pressurized steam to further pump the water. Thomas Newcomen's atmospheric engine was the first commercial true steam engine using a piston, and was used in 1712 for pumping in a mine.

In 1781 James Watt patented a steam engine that produced continuous rotary motion.^[1] Watt's ten-horsepower engines enabled a wide range of manufacturing machinery to be powered. The engines could be sited anywhere that water and coal or wood fuel could be obtained. By 1883, engines that could provide 10,000 hp had become feasible.^[2] Steam engines could also be applied to vehicles such astraction engines and the railway locomotives. The stationary steam engine was a key component of the Industrial Revolution, allowing factories to locate where water power was unavailable.

Steam engines are external combustion engines,^[3] where the working fluid is separate from the combustion products. Non-combustion heat sources such as solar power, nuclear power or geothermal energy may be used. The ideal thermodynamic cycle used to analyze this process is called the Rankine cycle. In the cycle, water is heated and transforms into steam within a boiler operating at a high pressure. When expanded through pistons or turbines, mechanical work is done. The reduced-pressure steam is then condensed and pumped back into the boiler.

In general usage, the term steam engine can refer to either the integrated steam plants (including boilers etc.) such as railway steam locomotives and portable engines, or may refer to the piston or turbine machinery alone, as in the beam engine and stationary steam engine. Specialized devices such as steam hammers and steam pile drivers are dependent on steam supplied from a separate boiler. Reciprocating piston type steam engines remained the dominant source of power until the early 20th century, when advances in the design of electric motors and internal combustion engines gradually resulted in the replacement of reciprocating (piston) steam engines in commercial usage, and the ascendancy of steam turbines in power generation.^[4] Considering that the great majority of worldwide electric generation is produced by turbine type steam engines, the "steam age" is continuing with energy levels far beyond those of the turn of the 19th century.